综述 ● 开放获取阅读更多

摘要

材料在切削加工、热处理、氢气及低温等条件下，会发生脆化，加工过程中材料脆化通常与应变率密切相关。在材料动态加载过程中，如高速加工，高应变率会导致材料脆化。为了明确应变率导致材料脆化的机理，本文围绕材料在高应变率下的动态力学响应问题，以及高应变率加载过程中应变率诱发材料脆化和碎化问题进行分析与探讨，首次提出了应变率敏感系数和伪脆化的概念，分别用于表征材料脆化随应变率的变化特征以及材料在超高应变率下的脆化特征，基于位错动力学讨论了应变率诱发材料脆化和碎化的内在机理。

1.引言

导致材料脆化的因素众多，例如三轴拉伸应力状态、热处理和低温条件等。表1列出了常见的材料脆化类型，其中高应变率会导致材料脆化，而高应变率是高速加工中的典型特征。焊接脆化与材料偏析和析出有关，焊接过程中“柯氏气团”的形成阻碍了位错运动并引起析出脆化1。此外，在钢的热处理过程中，由于碳原子和氮原子等会阻碍位错滑移，因此在一定温度下可能会发生蓝色脆化，从而导致材料强度提高2。低温脆化则是由位错运动的临界应力增加而导致的3, 4。氢脆是由于氢化物的产生或氢原子附着在裂纹尖端而引起的表面能降低的结果5。辐照脆化在核反应堆材料中很常见，因为辐照产生的点缺陷与溶质原子相互作用形成沉淀，阻碍位错运动并导致材料脆化6-8。

提高材料的强度和硬度或降低断裂韧性会导致材料脆化。在机械加工、子弹冲击、爆炸和隧道挖掘等过程中，存在应变率效应，材料性能会发生变化，如表2所示。Chilton等人9利用冲击压缩实验研究了钨在低温下的塑脆转变问题，发现材料的塑脆转变温度随应变率增加而增加，在一定温度条件下，材料随应变率增大而脆化。

在加工过程中，尤其是高速加工过程中，材料的应变率可达到10⁷s^-1，高应变率会导致材料脆化10。高应变率下的材料脆化为难加工材料的高效、高质量加工提供了一种有效途径。高速加工过程中由于材料脆化，提高了材料的可加工性，使传统加工中经常遇到的切屑瘤、砂轮堵塞等问题不复存在。

表 1  常见的材料脆化因素

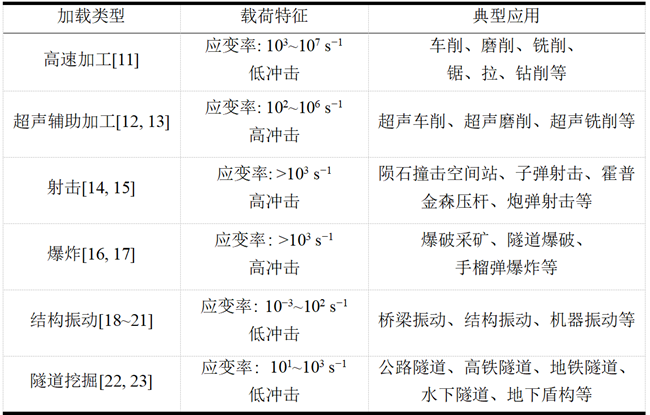
表 2  不同加载类型条件下的材料的应变率范围及其典型应用

难加工材料（硬脆材料、复合材料、钛合金、镍基合金等）通常具有良好的力学和物理特性，被广泛用于航空航天、国防、半导体、汽车和切削刀具等行业24-26。但是，这些材料很难加工，因为在加工过程中往往会产生工件的表面/亚表面损伤、较差的表面光洁度和尺寸精度、加工颤振以及切削磨损等问题。众多研究表明高速加工是解决难加工材料加工问题的有效方法，有助于提高加工效率和加工质量，并抑制表面和亚表面损伤27-29。现有研究表明，磨削过程中的材料脆化有助于减小加工表面损伤深度30, 31。因此，在高速加工过程中实现高应变率诱发材料脆化，有望解决传统加工过程中涉及的典型问题，如切屑瘤、砂轮堵塞、工件烧伤、毛刺形成、表面碎裂和表面完整性差（例如裂纹、残余应力、塑性变形和相变）等。然而，目前高应变率诱发材料脆化的机理尚不完全清楚，有待进一步研究32。

本文的研究重点是高应变率载荷下材料的脆化机理，第2节描述材料在高应变率下对动态载荷的响应。第3节主要分析高应变率下材料的脆化现象。第4节讨论应变率诱发材料脆化的机理。第5节对全文进行总结并得出结论。

2.材料在高应变率下的力学响应

为揭示高应变率条件下的材料脆化机理，有必要研究材料在高应变率载荷下的动态力学响应，分析应变率对材料力学性能的影响。本节将通过常见的高应变率实验方法和材料本构方程来分析材料对动态载荷的力学响应问题。

2.1.高应变率加载过程

高应变率实验方法常用于研究和分析材料在高应变率下的力学响应。分离式霍普金森压杆（SHPB）是常用的实验技术之一，它由撞击杆、放置试样的入射杆和透射杆组成。图1为SHPB的结构示意图，该技术广泛用于研究塑性和脆性材料在高应变率下的力学性能。通过采集冲击过程中的入射波、透射波和反射波，可以获得材料在高应变率下的动态力学性能。

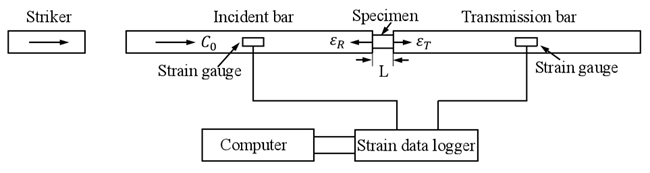
图1 SHPB的结构示意图 33

根据一维应力波和应力均匀性假设，可以通过公式获得材料在SHPB实验过程中的应变、应变率和应力，如公式（1~3）所示33，

\\varepsilon \left(t \right) = \frac2C_0L\int\limits_0^t \varepsilon _R\left(t \right)dt \ (1)

\\dot \varepsilon \left(t \right) = \frac2C_0L\varepsilon _R\left(t \right)\ (2)

\\sigma \left(t \right) = E\left(\fracAA_S \right)\varepsilon _T\left(t \right)\ (3)

其中ε_R和ε_T分别是反射应变幅值和透射应变幅值；A_s为试样的横截面积；L为试样长度； A为入射杆的横截面积；E为试样的杨氏模量；C₀是入射杆的弹性波波速。

此外，为准确获得材料在高应变率下的动态力学性能，众多学者还对SHPB装置进行了改进。Frew等人34在传统SHPB设备上采用脉冲整形技术对脆性材料进行了高应变率压缩试验。通过对入射脉冲进行整形，实现了在加载过程中既满足动态应力平衡又保证试样在恒定应变率状态下进行加载，动态压缩实验的准确性因此得以提高。此外，为研究材料在更高应变率下的力学响应，Liu等人35, 36通过强化压杆材料和减小压杆尺寸，搭建了应变率高达10⁴ s^-1的小型SHPB设备。然而，尽管SHPB技术已广泛应用于塑性和脆性材料的动态力学性能实验，但难以描述材料在更高应变率下（如在高速加工过程中，其应变率可达10⁷ s^-1甚至更高）的动态力学性能。

为此，Meyer等人37使用改进的SHPB装置对帽形试样进行了高速剪切实验，实验装置及试样形状如图2所示，并利用电子背散射衍射（EBSD）和透射电子显微镜（TEM）等技术研究了AISI 304L不锈钢的微观组织演变。实验结果表明试样的局部应变率增加到10⁴ s^-1以上，有利于研究在高应变率下材料的绝热剪切带内的微观组织演化机理。然而，由于该方法在加载过程中试样内部应力状态的复杂性，因此难以对加载过程中的应力、应变等进行定量分析，存在一定的局限性。

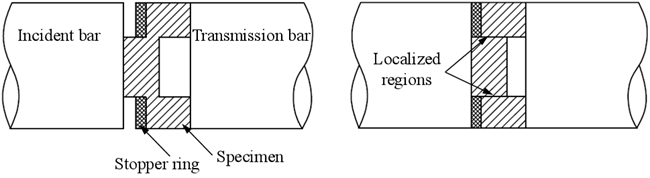
图2 实验装置及帽形试样示意图37

Sutter等人29使用改进的SHPB装置对TC4进行了高速正交切削实验，如图3所示，并利用应变片、高速相机等对高速切削过程的切削力、切屑形成等进行了检测。研究了切削速度对切屑形貌及切屑形成机理的影响，发现随着切削速度的提高，切屑由连续切屑变为锯齿形切屑。该实验方法可以实现速度约为75 m/s的高速正交切削，但切深等参数难以准确控制。

刘战强等人38在高速正交切削实验中研究了7050-T7451铝合金在120 m/s切削速度下的变形和断裂行为，实验装置如图4所示。研究结果表明切屑存在脆性断裂的特征，形成了崩碎切屑，且由于材料脆化导致了切削温度和切削力的降低。

此外，单点磨削40、超高速磨削31、板冲击实验41、SHPB拉杆实验42、三轴高速冲击试验43, 44、膨胀环技术45、摆锤冲击技术46、弹丸侵彻47, 48等多种动态加载实验技术也常用于研究材料对高应变率的响应。且随着高性能装备的飞速发展，尤其是高速机床的发展，高速加工技术有望实现更高应变率、更高精度的动态加载，将为研究材料在高应变率/超高应变率下力学性能提供技术保障。

图3 弹道冲击切削装置示意图29

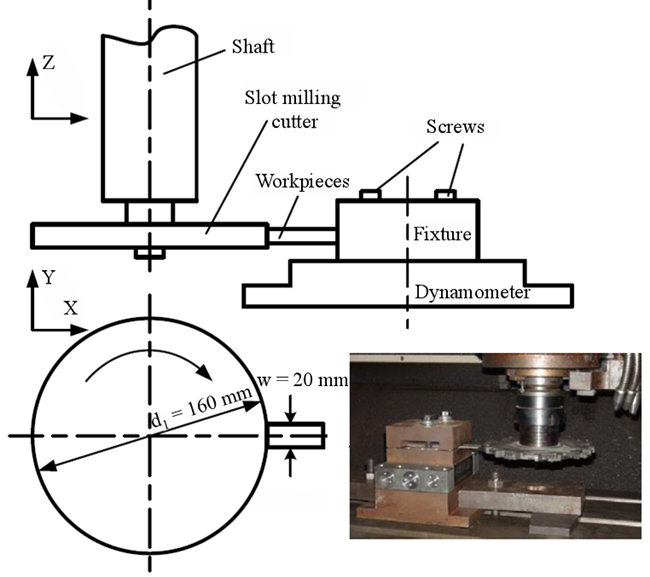
图4 高速正交切削装置39

2.2.高应变率下的材料本构方程

材料对动态载荷的响应与应力/应变场、应变率、温度场、预先存在的材料损伤以及周围环境等多个因素有关。由于影响因素众多，很难通过实验分析单个因素对材料动态力学性能的影响。因此，材料本构方程成为分析材料在高应变率下的力学响应的重要手段。材料本构方程主要分为经验性本构方程和物理性本构方程。常见的如Johnson - Cook（J-C）经验性本构方程以及基于位错动力学的物理本构方程等。

2.2.1.经验本构方程

J-C本构方程是描述材料动态力学性能的常用经验性本构方程，其形式如公式（4）所示49，

\sigma = \left(A + B\varepsilon ^n \right)\left(1\rm + C\ln \dot \varepsilon ^* \right)\left(1 - T^*m \right) (4)

其中σ为等效应力；ε为等效塑性应变；\dot\varepsilon^*=\dot\varepsilon / \dot\varepsilon_0是无量纲化的应变率，\dot\varepsilon_0为参考应变率；T^*=(T-T_r)/(T_m-T_r)为无量纲化的温度，T_m是材料的熔化温度，T_r为环境温度；A为材料在参考温度和参考应变率下的屈服强度；B是应变硬化系数；C为应变率硬化系数；n是应变硬化指数；m为热软化系数。

J-C本构方程考虑了应变、应变率和温度对材料动态力学性能的影响，具有较少的参数，便于求解，因此广泛应用于切削加工仿真当中。由于J-C本构方程是经验性方程，因此在不同的材料和载荷条件下本构方程会有所差别。为准确描述材料对动态载荷的响应，众多学者考虑各种因素的影响对J-C本构方程进行了修正，表3所示为常见的几种修正的J-C本构方程。

J-C本构方程对解决许多实际问题具有重要意义，广泛用于高应变率下材料的有限元仿真分析当中。但是该方程是应变、应变率和温度的解耦表达，在一定程度上影响了其预测精度。

对于脆性材料，Johnson等人提出了J-H本构方程56, 57来描述脆性材料在高应变率下的力学性能，如公式（5）所示

\\sigma ^\rm*\rm = \sigma _i^* - D\left(\sigma _i^* - \sigma _f^* \right)\ (5)

其中σ_i^*代表无损伤材料的归一化强度；σ_f^*是归一化的断裂应力；D为材料的损伤因子(0≤D≤1)，材料强度的无量纲表达式如公式（6）所示

\\sigma ^\rm*\rm = \sigma /\sigma _HEL\ (6)

其中σ_HEL是Hugoniot弹性极限处的等效应力。

无损伤材料的强度σ_i^*如公式（7）所示，

\\sigma _i^* = A\left(P^* + T^* \right)^N\left(1 + C \cdot \ln \dot \varepsilon ^* \right)\ (7)

其中A、C和N是待求的材料常数；\\sigma _i^* = A\left(P^* + T^* \right)^N\left(1 + C \cdot \ln \dot \varepsilon ^* \right)\是无量纲化的应变率，\\dot \varepsilon \为应变率，\\dot \varepsilon _0\为参考应变率；P*和T*分别是无量纲的压力和无量纲的材料最大拉伸强度，

\P^\rm*\rm = \fracPP_HEL\ (8)

\T^\rm*\rm = \fracTP_HEL\ (9)

其中P_HEL为弹性极限处的压力；P为实际压力；T为材料的最大拉伸强度。

出现损伤后的无量纲化的材料强度σ_f^*如公式（10）所示

\\left\ \beginarrayl\sigma _f^* = B\left(P^* \right)^M\left(1 + C \cdot \ln \dot \varepsilon ^* \right)\\\sigma _f^* \le \sigma _f\max ^*\endarray \right.\ (10)

其中B和M为材料常数；σ_fmax^*是材料无量纲化的断裂强度。J-H本构方程考虑了应变率及脆性材料的损伤等对材料力学性能的影响，目前已广泛用于脆性材料（如混凝土、陶瓷等）的工程设计当中。

表 3  修正的J-C本构方程

* 相关参数的具体含义请参考对应参考文献

2.2.2.物理本构方程

材料发生塑性变形的本质是位错的运动与滑移，理论上讲，如果材料中不存在阻碍（如晶界和第二相等），位错滑移速度会达到理论极限，即声速。但实际位错移动过程将受到各种因素的阻碍，材料的流动应力通常用公式（11）表示58，

\\sigma _y = \sigma _pn + \sigma _dis + \sigma _HP + \sigma _obs\ (11)

其中σ_pn为与温度和应变率有关的晶格阻力；σ_dis是位错间的相互作用力，\sigma_\text dis =G b \sqrt\rho，G 为剪切模量，b是Burgers矢量，ρ为位错密度；σ_HP为晶界对位错滑移的阻碍，可用Hall-Petch关系表示，\sigma_H P=k_y d^-1 / 2，k_y 为材料常数；d 为材料的平均晶粒尺寸；σ_obs为溶质原子、点缺陷等对位错的阻碍。

位错热激活理论常用于材料物理本构方程的研究当中。根据热激活理论，材料的流动应力σ_y可分为热相关的短程阻力σ_th和热无关的长程阻力σ_ath，

\\sigma _y = \sigma _th + \sigma _ath\ (12)

基于位错热激活理论，位错滑移的热相关的阻力随温度变化而变化，如图5所示，位错克服障碍进行滑移所需要的应力随着温度的增大而减小。为描述位错滑移所需要克服的障碍，Follansbee等人59 提出用p和q作为描述位错滑移所需克服障碍的形状参数，位错克服障碍所需的激活能如公式（13）所示60，

\\Delta G = \Delta G_0\left 1 - \left(\frac\tau \tau _0 \right)^p \right^q\ (13)

其中△G为位错克服障碍所需要的激活能；△G₀为在0 K时，位错克服障碍所需要的激活能；τ₀为0 K时的热激活应力；τ为热激活应力。

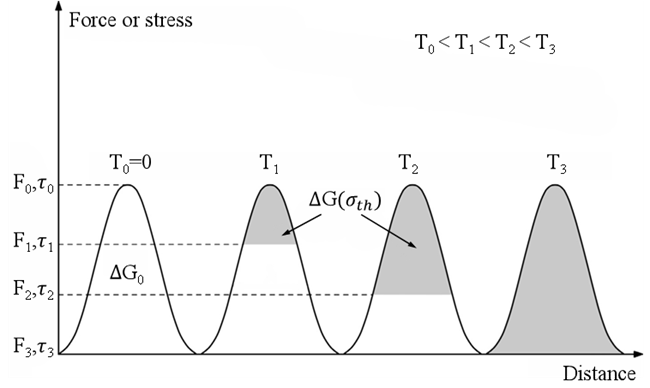
图5 热激活相关的位错障碍的示意图 60

根据位错的热激活理论，原子振动的幅度随温度增大而增大，当位错的能量超过障碍的能级时，位错以特定频率v（公式（14））成功越过障碍，进行滑移，

\v = v_0\exp \left( - \frac\Delta GkT \right)\ (14)

其中v₀ 为位错的振动频率；k 是Boltzmann常数；T 为温度；t_w= v^-1，t_w 为位错在障碍前等待的时间。位错在障碍物间滑移的速度v_f可以用公式（15）表示 61,

\b\sigma _f = Bv_f\ (15)

其中B 为位错拖曳系数；σ_f为位错滑移的驱动力，σ_f=σ_y-σ_ath。假设l 为障碍物间的平均距离，则位错在障碍物间滑移所需的时间t_f可用公式（16）所示，

\t_f = \fraclv_f\ (16)

位错滑移的平均速度如公式（17）所示62，

\V = \fraclt_w + t_f\ (17)

位错滑移过程中将受到位错拖曳力的影响，通常在低应变率状况下，t_w?t_f，位错拖曳力的影响可以忽略，然而在高应变率下，t_w≈t_f，位错拖曳力对流动应力影响显著，其影响不可忽略。基于位错的热激活理论，众多学者给出了多种描述材料在高应变率下塑性变形的物理本构方程，如表4所示。与经验性本构方程相比，物理本构方程有助于从位错等微观角度深入理解应变率对材料性能的影响，但物理本构方程一般较为复杂，参数较多，不易求解，限制了其在工程实际中的应用。

表4  高应变率下的材料物理本构方程

*相关参数的具体含义请参考对应参考文献

2.3.动态载荷下的材料响应

图6为基于不同材料本构方程得到的应变率对材料屈服强度的影响结果。实线拟合的黑色数据点和虚线拟合的白色数据点分别是基于物理本构方程和经验本构方程得到的计算结果。物理本构方程的结果表明，当应变率超过约10⁴s^-1时，材料的屈服强度会迅速增加，这也与众多学者的实验结果相吻合，同时大量研究还表明材料强度的迅速增大与位错拖曳力的影响密切有关，当应变率达到一定值时，位错拖曳力对材料强度的影响不可忽略，并将成为主导因素68-71。图6结果还表明，与J-C本构方程相比，基于物理的材料本构方程能更准确地描述应变率对材料性能的影响。

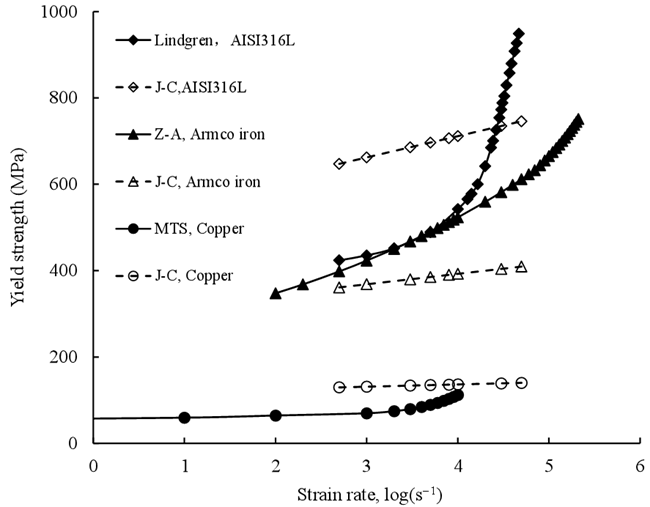
图6 不同本构方程得到的材料屈服强度随应变率的变化情况 49, 63, 64, 66, 72-74

图7给出了单晶铝的剪应变率对剪切应力影响的实验结果。尽管材料不存在第二相和晶界等的影响，但实验结果表明，位错拖曳力对单晶铝的影响同样显著，表明位错拖曳力的影响与位错间相互作用力和晶格阻力等密切相关。

众多结果表明，材料强度如材料的屈服强度和极限抗拉强度等都会随应变率的增加而增加。同时，Zhou等人31还指出材料的屈服强度随着应变率的增长速度要大于材料极限抗拉强度随应变率增大的速度，因此，随应变率增大，材料的屈服强度逐渐接近材料的极限抗拉强度，当材料的屈服强度与材料的极限抗拉强度相当时，材料未发生塑性变形就发生断裂，材料脆化。假设材料的极限抗拉强度与屈服强度之差为\Delta \sigma ，

\Delta \sigma \rm = \sigma _UT - \sigma _Y (18)

其中\sigma _UT为材料的极限抗拉强度；\sigma _Y为材料的屈服强度。根据众多学者在高应变率下的拉伸实验结果42, 76-80得到了不同材料的\Delta \sigma 随应变率的变化情况，如图8所示。根据图8，\Delta \sigma 与应变率之间的关系可由公式（19）表示，

\Delta \sigma \rm = k_0 - k_s\ln \dot \varepsilon (19)

其中k₀是材料常数，k_s表示材料脆化的应变率敏感性系数，两者的单位取MPa。对于不同的材料，材料在\Delta \sigma \rm = 0处发生塑脆转变。根据图8所示的k_s值，材料可以分为三种类型：I、II和III，其中I型材料的k_s最大，因此最容易在高应变率下脆化，而III型材料k_s较小，对应变率最不敏感，在高应变率下最不易脆化。如TC4和DP1000为I型材料，其应变率敏感性系数分别为35.4 MPa和45.9 MPa。在加载过程中其\Delta \sigma 随应变率的增大而迅速减小，当\Delta \sigma =0时，材料脆化。相反，7075-T6和6061-T6属于III型材料，其k_s值分别为1.5和0.4。即使在非常高的应变率下，材料脆化也难以发生。对于具有相同k_s的材料，k₀越大，材料脆化所需的应变率越高。

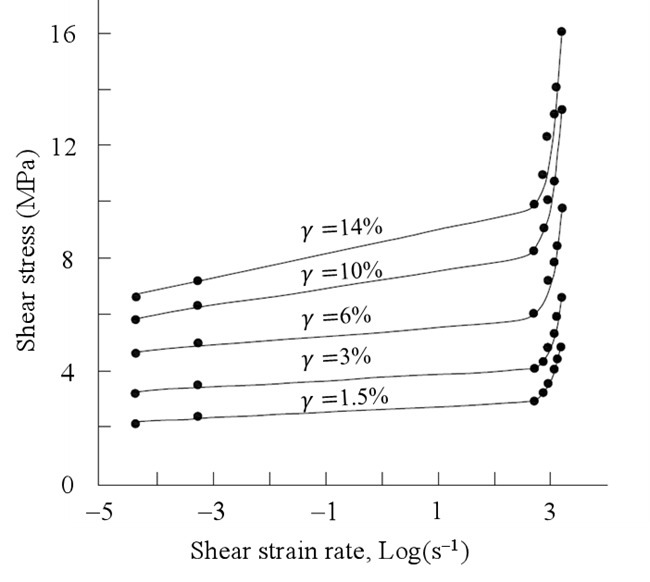
图7 实验得到的单晶铝的剪应力随剪应变率的变化情况75

应变率对脆性材料力学性能的影响同样显著，针对脆性材料的高应变率实验研究也受到国内外学者的广泛关注，其中SHPB技术常用于研究高应变率下脆性材料的动态力学性能。Harsha等人81利用SHPB技术并基于裂纹扩展动力学，将裂纹速度与裂纹尖端的应力瞬时值相关，建立了的微机械动力学本构方程。实验与仿真结果如图9所示，可见当应变率增加到10³ s^-1时，大理石材料的强度同样迅速增大，有研究指出这是由于与裂纹尖端传播相关的非线性和惯性效应的相互作用可能会产生阻力，进而阻碍裂纹扩展，导致材料强度提高82, 83。

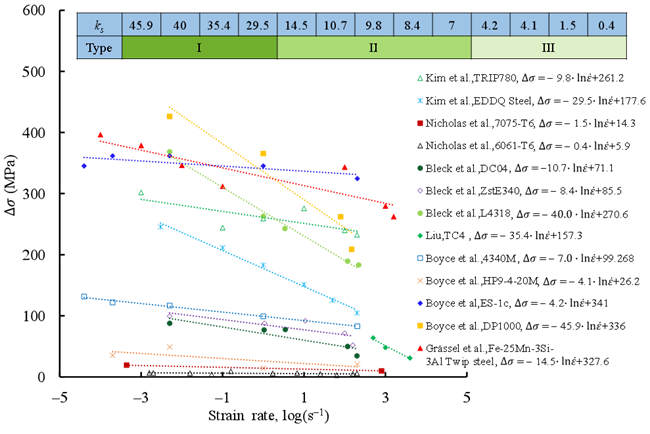
图8 应变率对 ∆σ的影响42, 76-80

Li等人84研究了花岗岩的强度和碎片尺寸在冲击载荷下随应变率的变化情况，发现随应变率的增大，花岗岩的强度增加，但碎片尺寸减小。图10为铝硅酸盐玻璃在冲击试验中得到的结果，实验得出了类似的结论85。针对高应变率下的材料碎化问题，Grady和Kipp等人86认为在较高的应变率下，冲击载荷会激活材料内部更多的缺陷，从而产生较小的碎片尺寸，导致材料碎化。

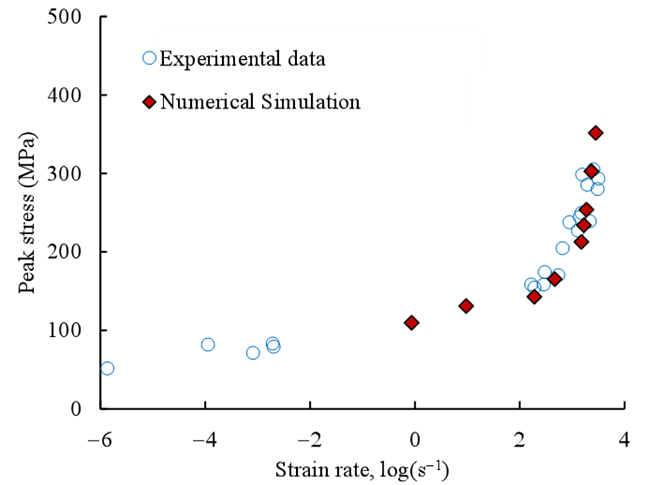
图9 应变率对大理石强度的影响 81

对于金属玻璃类的非晶材料，应变率同样会显著影响材料性能87, 88。Lu等人89分别使用准静态和动态SHPB加载装置研究了Zr基大块金属玻璃的静态和动态力学性能，结果表明材料强度随应变率增加而增大。Yu等人90对具有不同应变率和温度的La基金属玻璃进行了拉伸测试，发现应变率的增加会促进金属玻璃的脆化。Liu等人35使用一种改进的SHPB装置对Zr基块状金属玻璃进行动态压缩实验，发现材料的超塑性随着应变率的增加而消失。因此，应变率的增加同样可能导致非晶材料的材料脆化。上述研究表明，应变率增大会导致材料强度的增大以及材料脆化。

图10 未增强的铝硅酸盐（ALS）玻璃的动态压缩实验的结果，(a) 静态和动态实验得到的应力-应变曲线；(b) 最大抗压强度随应变率的变化；(c) 由静态和 (d) 动态载实验中得到的材料碎片和碎屑85

3.高应变率下的材料脆化

3.1.加工中的材料脆化

在高速加工、超声辅助加工及隧道挖掘等过程中，由于应变率的影响，同样存在材料脆化和碎化现象。如图11所示，在正交切削过程中，随着切削速度的增大，切屑由连续性切屑变为非连续性切屑。在高速加工中，应变率高达10⁷s^-191-93，导致高速加工中的材料去除机理与传统切削加工有较大差别。Wang等人94研究了高速加工过程中的材料塑脆转变问题，发现随着应变率的增大，切屑由连续性切屑变为节状切屑，且切屑存在脆性断裂特征。Ma等人95利用轻气炮装置进行了TC4的高速正交切削实验，发现在切屑自由表面存在脆性断裂特征，且随着切削速度的增大，脆性断裂特征增加，而韧性断裂特征减少。

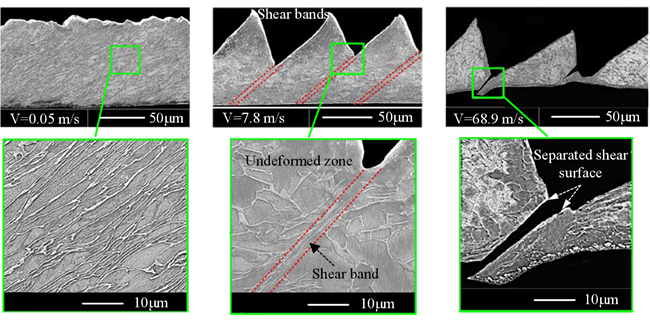
图11 不同切削速度下TC4的切屑形貌96

超声辅助加工广泛用于加工各种不同材料（尤其是硬脆材料），在超声辅助加工过程中，刀具与高频振动叠加在一起，从而获得比常规切削过程中更高的瞬时切削速度和加速度。较高的切削速度和加速度会导致较高的应变率，同样可能引起加工过程中的材料脆化。针对超声辅助加工的影响，Zhao等人97研究了岩石的超声辅助加工，发现冲击频率的增加会显著增加材料的碎化。Lv等人98研究了BK7玻璃的超声辅助加工，发现超声振动会导致材料碎化，并使加工过程中的切削力降低。在对K9玻璃的超声辅助加工实验研究中，Wang等人99发现，与传统加工相比，超声辅助加工可以将亚表面损伤的深度降低30~40％。

由于超声辅助加工过程涉及高应变率，因此在超声辅助的加工过程中材料可能会脆化和碎化。如图12所示，应变率对材料脆化和加工表面损伤的影响可能与如下因素有关：

（1）裂纹尖端的材料阻力会随着应变率的增加而增加，阻碍了裂纹的扩展，降低了加工表面损伤深度。

（2）在加工过程中切削方向和中位裂纹扩展方向不同。因此，在较高的切削速度下，中位裂纹（如果成核）在切削刀具通过之前传播的时间更少，从而导致亚表面损伤深度较小。

（3）材料的内部缺陷在冲击载荷下被激活，这会导致微裂纹的形核、扩展和相互交叉，并在材料的表层中产生更多的裂纹，导致材料碎化。

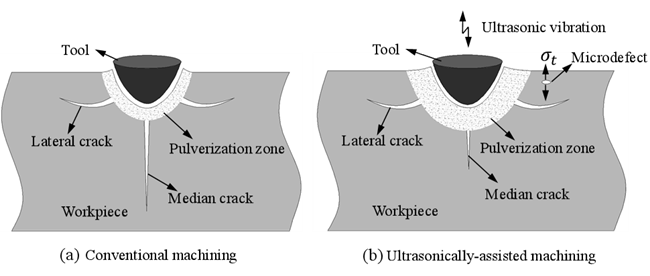
图12 传统加工与超声辅助加工引起的材料损伤的对比示意图

盾构机（TBM）常用于地铁、火车等的隧道挖掘中，在隧道的掘进过程中通常需要切削岩石等硬脆材料，同样存在应变率效应，可能导致材料的脆化和碎化。有研究表明，在掘进过程中，通过应变率效应可以增强岩石的脆性，显着影响岩石的可加工性。Kahraman等人100研究了材料脆性的测量方法以及岩石的脆性与可加工性之间的关系，并提出在TBM的挖掘性能和岩石的脆性之间应该有指数关系。Gong等人101研究了岩石脆性对TBM渗透率的影响，发现碎裂区和径向裂缝随岩石脆性的增加而增加，而刀具引起的破碎几乎随岩石脆性线性增加。为了提高加工效率并减少刀具磨损，Wu等人102提出了一种冲击扰动的碎石方法，并建立了冲击诱导孔周围岩石损伤区的裂纹模型，观察到刀具穿透率随裂纹密度增加而增加，而切削力随扰动频率的增加而减小。由此可见，通过提高应变率来增加岩石脆性有利于改善隧道掘进过程中的加工效率和材料的可加工性。

此外，为研究高应变率下的材料碎化问题，Zhang等人还建立了高应变率下脆性材料的碎片尺寸S的预测模型103，如公式（20）所示，同样可以看出碎片平均尺寸大小随应变率的增加而减小，

\S = \frac6K_IC^2D_fE^2\dot \varepsilon ^2t_f^2\ (20)

其中K_IC 为材料的断裂韧性；D_f表示与碎化开始相对应的损伤标量；E 为杨氏模量；t_f 为达到断裂应力所需的总时间。此外，Grady和Kipp等人104 搭建了针对塑性材料的膨胀环实验，并基于断裂能理论计算了材料的碎片尺寸S，如公式（21）所示，

S=2 x\left(t_c\right)=\left(\frac12 \gamma_s\rho_0 \dot\varepsilon^2\right)^1 / 3 (21)

其中γ_s为材料的表面能，ρ₀为材料密度。同样可以看出，碎片尺寸随应变率的增大而减小。

3.2.应力波对材料碎化的影响

应力波是影响高应变率下材料碎化的重要因素。材料碎化与应力波的传播、反射及相互作用过程密切相关。Zhang等人105认为，冲击载荷引起的应力波响应是硬脆材料中材料去除和裂纹形成的主要原因。根据应力波在固体中的传播状态，应力波传播有不同的形式，如弹性波、塑性波和粘弹性波等。弹性波和塑性波的传播速度如公式（22）和（23）所示106，

\v_e = \left(\fracE\rho _0 \right)^1/2\ (22)

\v_p = \left(\frac1\rho _0\fracd\sigma d\varepsilon \right)^1/2\ (23)

其中E 为材料的杨氏模量；dσ/dε是对应于应力-应变曲线上应力点σ的切线的斜率；ρ₀为材料的密度。可以看出材料的应力波传播速度与材料在冲击载荷下的力学性能密切相关。

研究表明在冲击载荷下产生的应力波会在材料内传播，并在自由面产生反射，形成拉伸波，进而导致材料损伤。图13所示为波长λ的压缩方波在杆端自由面反射时的不同时刻的压力分布107。图13（a）表示压缩波接近自由面；（b）表示入射压缩波与反射拉伸波叠加，形成复合波，重叠区域（蓝色）出现拉应力；（c）表示复合波全部为拉伸波，此时为临界状态，在此之前，试件仍受部分压应力作用，在此之后，试件完全受拉应力作用；（d）重叠区域逐渐减小，拉应力降低；（e）入射压缩波消失，应力波反射结束。

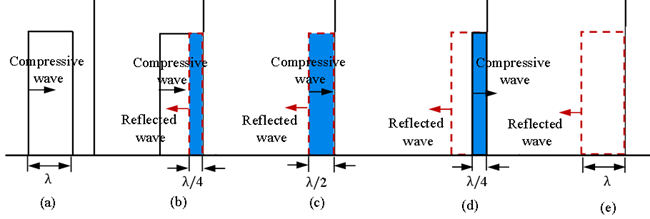
图13 压缩应力波的传播及其在自由表面的反射107

如图14所示，姜峰等人108通过SHPB对花岗岩进行冲击压缩试验，研究了在冲击载荷下花岗岩的断裂特性。发现入射压缩波在自由面的反射会产生拉伸波，并在自由面附近引起拉应力，导致裂纹形核和扩展，最终使试样后部的材料碎化。

图15为圆柱顶部受到冲击载荷时的应力波传播过程。如图15（c）所示，在冲击载荷过程中会形成裂纹，其中OA裂纹（心裂）是由于反射的拉伸波在圆柱中部相遇而引起的；BC裂纹是由于从圆柱表面反射的拉伸波引起的；EF裂纹是由底面的反射拉伸波引起的；拉伸波从底部反射与圆柱两侧反射拉伸波在底角处相遇形成裂纹LM。如图16所示，图15中的裂纹系统可以通过受冲击载荷的花岗岩的材料碎裂来证明。在冲击载荷下，花岗岩具有径向裂纹（从冲击中心向外延伸）和以撞击点为中心的环向裂纹。当冲击载荷足够大时，各种裂纹相互交错,最终形成块状碎屑。

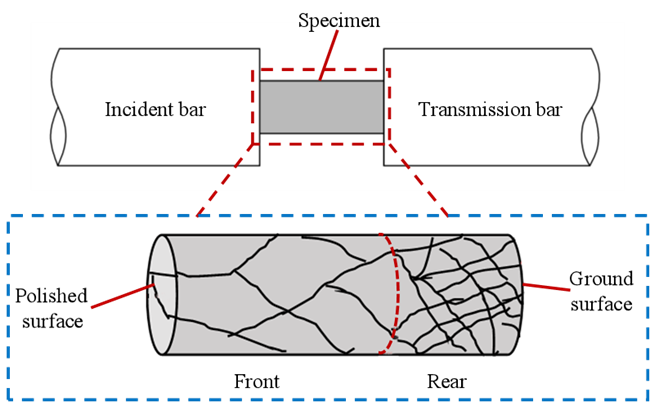
图14 花岗岩在高应变率下的断裂特征示意图108

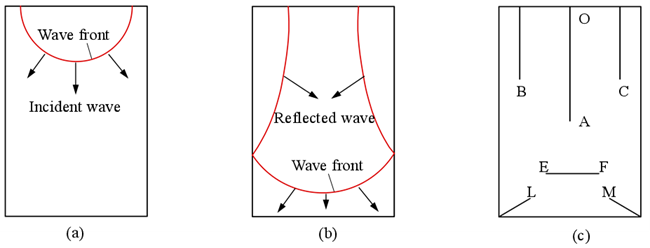
图15 圆柱顶部受冲击载荷时的应力波传播特性107

图16 计算机辅助断层扫描（CT）图像：(a) 灰度图；(b) 裂纹图像 109

在塑性材料中，应力波同样会导致材料脆化和碎化。Liu等人110对钛合金靶材进行了子弹冲击实验，如图17所示。图17（a）和（c）分别为子弹冲击实验中样件的截面图及仿真结果。由图17（a）可以看出，在I区和III区没有明显的塑性变形，而是由冲击载荷导致的脆性断裂为主。同时，图17（c）的仿真结果表明在区域I和III中存在较大的拉伸应力，说明应力波传播在自由面的反射产生了拉应力，并导致了材料脆化，验证了在冲击试验中得到的实验结果。

图17 TC4靶材的宏观断裂特性，(a) 断裂特征；(b) 子弹形貌；

(c) 子弹冲击过程中，第一主应力在靶材中的分布特征110

Zheng等人111同样以820 m/s的冲击速度对TC4进行了子弹冲击实验，研究了TC4材料的破坏机理，发现TC4材料由于子弹侵彻而留下了许多微裂纹，如图18所示，并认为微裂纹扩展和聚集成了宏观裂纹，导致TC4材料在弹孔周围区域变脆。此外，由图18还可以看出，弹孔周围的材料被子弹推动和挤压，并在材料中沿纤维/层状层留下大量裂纹，而纤维/层状层的形成可能是由于在子弹穿透过程中，由弹头引起的拉伸应力与弹丸主体的压缩应力综合作用的结果。

图18.  TC4靶材截面（存在大量裂纹）光学显微照片111

3.3.高应变率下材料脆化的临界条件

材料脆化的临界条件是实现其实际应用的重要前提，针对材料脆化的临界条件，Rice和Thomson等人112 从原子级别尖锐的裂纹尖端的位错发射角度建立了晶体材料脆性断裂的临界条件，指出当满足公式（24）所示条件时，材料就会脆化，

\Gb/\gamma _s \ge 7.5 - 10\ (24)

其中G 为剪切模量；b 为Burgers矢量，然而由于材料的表面能难以准确获得，限制了公式（24）的应用。

在对高速磨削加工过程中材料塑脆转变问题的研究中，Zhou等人31指出，当切削速度超过塑性波传播速度时，材料脆化，如公式（25）所示，

\v_c > v_p = \left(\frac1\rho _0\fracd\sigma d\varepsilon \right)^1/2\. (25)

此外，Wang等人113研究了高速正交切削过程中的材料脆化现象，同样指出当切削速度超过塑性波传播速度时，材料脆化。该临界条件的提出对于指导高速加工具有重要的意义，然而，将塑性波的传播速度作为材料塑脆转变的临界切削速度，可能存在以下问题：

（1）应变率与切削速度成正比，切削速度的增大会导致材料力学性能的变化，进而改变材料的塑性波传播速度。

（2）材料的微缺陷和应力状态对材料的损伤形成和断裂有重要影响，仅用临界切削速度很难准确地描述材料的塑脆转变临界条件。

对于脆性材料，Lawn等人114首次使用硬度H与韧性K_f之比B来描述硬脆材料的脆性。在此基础上，Zhang等人30研究了硬脆材料的脆性与表面损伤深度之间的关系，首次提出了表面损伤深度与材料脆性成反比的结论。

研究塑性材料的屈服强度与韧性之间的关系，需要了解材料的断裂应变等随应变率的变化情况。Campbell等人115研究了应变率\dot \varepsilon 、温度T和晶粒尺寸D对En2A钢的拉伸断裂应变的影响，发现拉伸断裂应变随应变率的增加而降低，如图19所示。Mahalingam等人116在镍基金属的冲击实验中，研究了材料的塑脆转变问题，发现随着应变率的增大，材料出现脆性断裂特征，材料更加碎化，认为材料随应变率增大发生了塑脆转变。Abushawashi等人117研究了切削过程中应变率对材料断裂应变的影响，并根据J-C损伤模型计算了材料的断裂应变，如公式（26）所示：

\\varepsilon _f = C_1e^C_2\eta _f\left 1 + C\ln \left(\frac\dot \varepsilon \dot \varepsilon _0 \right) \right^\frac - 2n + 2\ (26)

其中，C₁ 和 C₂ 是通过实验得到的材料的断裂常数；\eta _f是描述材料应力状态的参数。

根据材料的本构方程\sigma \rm = f(\varepsilon,\dot \varepsilon,T)和材料的断裂应变\varepsilon _f，可以得到与应变、应变率和温度相关的材料的断裂韧性，如公式（27）所示，

\K_f = \int\limits_0^\varepsilon _f f\left(\varepsilon,\dot \varepsilon,T \right)d\varepsilon \ (27)

图19 应变率、温度和晶粒尺寸对En2A钢的拉伸断裂应变的影响 115。

根据2.3节内容，如图20所示，应变率的增加导致屈服强度的增加，材料的韧性降低，进而导致材料脆化。因此，材料脆性B可以用屈服强度\sigma _Y和材料韧性K_f的比值表示，如公式（28）所示，

\B = \frac\sigma _YK_f\ (28)

其中\sigma _Y = f\left(\varepsilon,\dot \varepsilon,T \right)_0.2\% ，在0.2% 应变时，可忽略应变硬化和温升的影响，因此材料的屈服强度公式可以简化为\sigma _Y = f\left(\dot \varepsilon \right)_0.2\% ，由公式（27）和（28），材料的脆性可由公式（29）表示，

\B = \fracf\left(\dot \varepsilon \right)_0.2\% \int\limits_0^\varepsilon _f f\left(\varepsilon,\dot \varepsilon,T \right)d\varepsilon \ (29)

然而，材料强度并不随应变率而保持持续迅速增加的趋势，而是存在一定的强度极限，如图20所示，红色虚线表示材料强度随应变率变化的趋势。如果材料以极高的应变率加载，则可能会达到材料的强度极限。

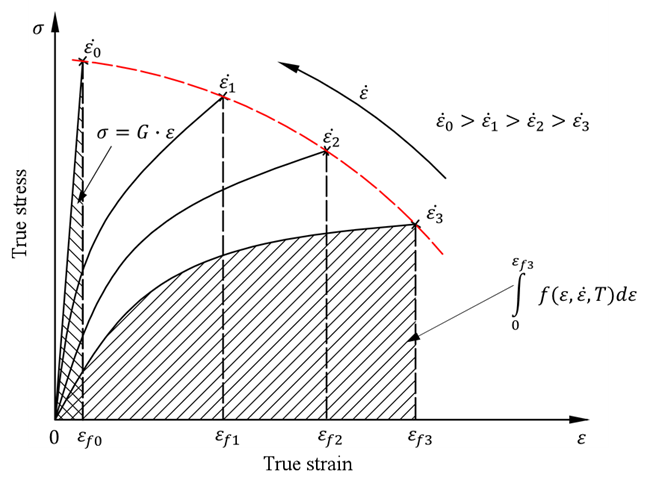
图20 应变率对材料强度和韧性影响示意图。

3.4.裂纹形核与扩展

材料的脆性断裂源自裂纹的形核和扩展。原子键断裂是裂纹成核和扩展过程中的重要特征，也是导致材料脆性断裂的主要因素。材料的理论断裂强度σ_m可由公式（30）求得，

\\sigma _m = \left(\fracE\gamma _sa_0 \right)^1/2\ (30)

其中E为材料的杨氏模量；\gamma _s为材料的表面能；a_0为材料的晶格常数。

针对材料的理论断裂强度远大于材料的实际断裂强度的原因，Griffith等人118认为由于材料内部存在缺陷降低了材料的断裂强度，并提出了裂纹扩展的Griffith断裂准则，如公式（31）所示，

\\sigma _c = \left(\frac2E\gamma _s\pi c \right)^1/2\ (31)

然而，Griffith断裂准则仅适用于脆性材料。为此，Orowan等人119 对Griffith断裂准则进行了修正，指出裂纹尖端扩展所消耗的能量不止是材料的断裂表面能γ_s，还有塑性变形能γ_p。进而提出了裂纹扩展的临界条件，如公式（32）所示，

\\sigma _c = \left(\fracE\left(2\gamma _s + \gamma _p \right)\pi c \right)^1/2\ (32)

为分析裂纹在塑性材料中的扩展机理，Stroh等人120 认为位错塞积是微裂纹形核的主要原因 (图 21)。并指出当在位错塞积位置的最大拉应力σ_fmax达到材料的理论断裂强度σ_m时，裂纹将会形核，进而提出了裂纹扩展的临界条件，如公式（33）所示，

\\tau _c = \tau _i + \left(\frac2Er\gamma _sda_0 \right)^1/2\ (33)

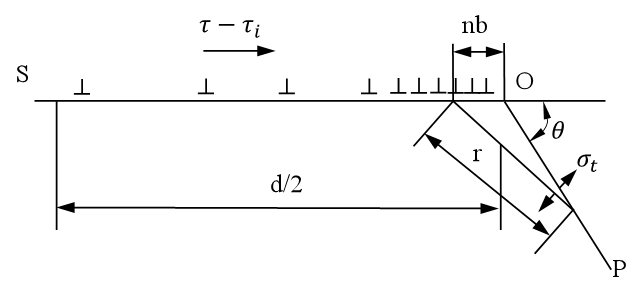
图21 位错塞积导致微裂纹形核

其中 d/2 代表位错源到位错塞积位置的距离；r 为位错塞积点到裂纹尖端的距离； τ-τ_i为滑移面上的有效剪切应力。

基于位错反应理论, Cottrell等人121从能量角度提出了裂纹扩展的临界条件，指出其临界应力为，

\\sigma _c = \frac2G\gamma _sk_yd^1/2\ (34)

考虑Hall-Petch关系和应力状态的影响，裂纹扩展的临界条件如公式（35）所示，

\\left(\sigma _id^\frac12 + k_y \right)k_y > 2G\gamma _sq\ (35)

其中 q 是与应力状态有关的系数。

此外，由于金属玻璃等非晶材料的原子结构是长距离无序的，通常不具有位错和晶界，因此它们的变形和断裂行为不同于晶体材料，但其变形和断裂同样与应变率和温度密切相关122。高应变率和/或低温会导致金属玻璃的不均匀变形，导致变形应变集中在薄至10~100 nm 123~125的空间层（剪切带）中。而剪切带的形成和扩展是金属玻璃中变形和裂纹形成的主要原因88, 126。

4.讨论

通常，高应变率会导致位错塞积，从而阻止位错运动，产生应力集中，使原子结合键断裂，从而导致裂纹形核并扩展，进而导致材料脆化。微观上，位错在低应变率加载过程中有足够的时间克服障碍，材料会发生塑性变形。当应变率足够高时，由于位错来不及滑移会导致位错塞积，从而引发裂纹成核。因此，在塑性材料的高速加载过程中，如果应变率足够高，以致在材料断裂之前不会发生塑性变形，则材料将发生脆化。在这种情况下，塑性材料将会像脆性材料一样，表现出脆性断裂的特征。对于以高应变率加载的脆性材料，应变率的增大同样会导致材料脆性增大。在对陶瓷材料的磨削研究中，Zhang等人127证实了陶瓷材料的脆性随应变率的增加而增加。

裂纹的形核和扩展与位错密切相关。在裂纹扩展过程中，裂纹尖端会发射位错，这些位错会受到微观障碍物（例如晶界）的阻碍，从而产生位错塞积，导致微裂纹形核。另一方面，由于裂纹尖端总是伴随着位错，所以位错密度成为影响裂纹扩展的重要因素。通常，位错密度越高，裂纹扩展越容易，原因是新的位错可能会被裂纹尖端的现有位错所阻碍，从而形成位错塞积，并产生应力集中，最终导致裂纹扩展。Jones等人128在实验研究中也证实了这一点，他们研究了存在应变硬化的TC4薄板中裂纹的形核及扩展问题，发现应变硬化可以加速疲劳裂纹的扩展。

应力波传播是导致高应变率下材料碎化的重要因素。冲击载荷会导致应力波从冲击载荷源产生和传播，并在自由面反射成为反射波，如图13所示，入射波和反射波之间的相互作用会引起拉应力，进而导致裂纹成核和扩展。如在高速切削加工过程中，由于冲击载荷的作用，在加工区中会引发应力波传播，并由工件的自由面反射形成反射波，入射波和反射波引起的拉应力会导致裂纹成核和材料碎化。

宏观上，加载过程中应变率的增大导致材料强度和硬度的增大，但材料的韧性降低，材料脆化。例如对于TC4材料，它是一种典型的两相合金（α相和β相），其中α相是密排六方结构，具有很少的滑动系统，位错不容易滑移。因此，在较高的应变率下，TC4材料中容易产生位错塞积，导致裂纹形核和扩展，并最终导致材料脆化。相反，铝是面心立方金属，具有更多滑移系统，且层错能较高，材料在加载过程中较容易产生塑性变形。因此，在铝中不容易引起位错塞积和材料脆化。

材料在高应变率动态载荷下发生脆化，如在高速加工过程中，在高应变率下部分可动位错没有足够的时间滑移，从而变为不可动位错，并阻碍其他位错的滑移，导致位错塞积和材料脆化，而在非加载状况，材料仍保持静态属性，并不表现出脆性，即材料受加载过程的影响表现出伪脆性。材料的伪脆化有助于抑制加工中工件的塑性变形和加工损伤，极大地保持加工的表面完整性。

本文提出的应变率敏感性系数k_s为确定材料脆化随应变率的变化状况提供了指导。以TC4为例，其应变率敏感系数为35.4，在图8中列出的金属材料中属于高应变率敏感性材料，在高应变率下更容易脆化，因此它更适于用高速加工的方法进行加工，进而实现高质量、高效率加工。

具有低应变率敏感性系数k_s的材料可以用于吸收冲击能量。如由铝合金和陶瓷制成的装甲，可以吸收弹丸的能量129-131。因为铝合金在图8所示的所有材料中具有最低的应变率敏感性系数，所以当在高应变率下承受载荷时，铝合金材料不易脆化。从而使该装甲既具有铝合金出色的塑性变形能力进而可以吸收能量，同时还具有陶瓷的抗渗透性，从而提高了装甲对高速子弹冲击的防护能力。温度升高是影响材料脆化的另一个重要因素，尤其是在切削加工过程中，塑性变形导致温度升高，有利于位错运动，但不利于材料脆化。为了研究由于应变率效应引起的材料脆化，必须使温度效应最小化。Salomon132首次提出在加工过程中，随着切削速度的提高，切削温度逐渐升高，而当切削速度达到一定值时，切削温度反而会急剧降低，然而，Salomon的预测至今尚未得到验证。因此，目前需要通过更高的切削速度及改变切深等方式来进一步研究高速加工中应变率对材料加工的影响，深入探讨Salomon预测模型的准确性。

在材料的物理和经验本构方程中，应变率是影响材料力学性能的重要因素，尤其是在高应变率下，通常需要考虑应变率的影响。本文分析结果表明，与J-C本构方程相比，物理本构方程可以更准确、更深入地分析和预测材料在高应变率下的材料力学性能。但基于物理的本构方程通常较为复杂，参数求解困难，限制了其实际应用，有必要对现有的本构方程进行修正或建立新的材料本构方程。

5.结论

本文主要分析了材料的脆化机理，以及基于应变率效应的材料塑脆转变的临界条件，并得出以下结论：

（1）高应变率加载时会发生材料脆化和碎化；

（2）应变率敏感性系数k_s是材料的固有特性，可用于评估材料脆化对应变率的敏感性；

（3）应变率敏感性系数低的材料不易发生材料脆化，反之亦然；

（4）应变率敏感性系数是选择特定应用材料的重要指标，例如在穿甲防护和高速加工等领域；

（5）在加载过程中，应力波的传播和反射会引起材料的脆化和碎化。

应变率诱发的材料脆化广泛存在于切削加工、隧道挖掘和装甲防护等领域。如果能够揭示在高应变率下材料脆化的机理，对于各种材料的实际工业应用将具有重要的指导意义。例如，在难加工材料的加工中，应变率导致脆化可以解决许多难加工材料（如钛合金、航空合金、高温合金、半导体和陶瓷等）的加工问题，将会大大提高工件的加工质量和加工效率。然而，目前尽管已有针对应变率导致材料脆化的研究，但其机理尚不明确，高应变率下材料的位错动力学、裂纹形核与扩展等相关机理仍不清楚，需要做进一步研究。

致谢

本文作者对国家自然科学基金委员会（项目号：51575084）和深圳市科创委（项目号：KQJSCX20180322152221965）的经费支持表示由衷感谢。

参考文献

1 Cottrell, Dislocations and plastic flow in crystals, Alan Howard, 1953.

2 Koyama M, Shimomura Y, Chiba A, Room-temperature blue brittleness of Fe-Mn-C austenitic steels, Scripta Materialia, 2017, 141: 20-23.

3 Stepanov N, Tikhonovsky M, Yurchenko N, Effect of cryo-deformation on structure and properties of CoCrFeNiMn high-entropy alloy, Intermetallics, 2015, 59: 8-17.

4 Darnbrough J, Roebuck B, Flewitt P, The influence of temperature and grain boundary volume on the resistivity of nanocrystalline nickel, Journal of Applied Physics, 2015, 118(18): 184302.

5 Xing X, Yu M, Chen W, Zhang H, Atomistic simulation of hydrogen-assisted ductile-to-brittle transition in α-iron, Computational Materials Science, 2017, 127: 211-221.

6 Toyama T, Nagai Y, Tang Z, Nanostructural evolution in surveillance test specimens of a commercial nuclear reactor pressure vessel studied by three-dimensional atom probe and positron annihilation, Acta materialia, 2007, 55(20): 6852-6860.

7 Pons D, Bourgoin J, Irradiation-induced defects in GaAs, Journal of Physics C: Solid State Physics, 1985, 18(20): 3839.

8 Kameda J, Bevolo A, Neutron irradiation-induced intergranular solute segregation in iron base alloys, Acta Metallurgica, 1989, 37(12): 3283-3296.

9 Chilton A, Wronski A, The effects of strain rate and pressurization on the ductile-brittle transition temperature of polycrystalline sintered tungsten, Journal of the Less Common Metals, 1969, 17(4): 447-450.

10 Wang B, Influence mechanism of material deformation and fracture behavior on chip formation during high-speed machining, Shandong University, 2016.

11 Wang B, Liu Z, Su G, Investigations of critical cutting speed and ductile-to-brittle transition mechanism for workpiece material in ultra-high speed machining, International Journal of Mechanical Sciences, 2015, 104: 44-59.

12 Hocheng H, Tai N H, Assessment of ultrasonic drilling of C/SiC composite material, Composites Part A: Applied Science and Manufacturing, 2000, 31(2): 133-142.

13 Tawakoli T, Azarhoushang B, Influence of ultrasonic vibrations on dry grinding of soft steel, International Journal of Machine Tools and Manufacture, 2008, 48(14): 1585-1591.

14 Iqbal M A, Gupta G, Diwakar A, Effect of projectile nose shape on the ballistic resistance of ductile targets, European Journal of Mechanics-A/Solids, 2010, 29(4): 683-694.

15 Klavzar A, Pursche F, Herzig N, Wolf T, Ballistic Limit Thickness and Failure of Steel Targets with Different Strengths under EFP Impact, Procedia Engineering, 2017, 197: 270-277.

16 Hiroe T, Fujiwara K, Hata H, Takahashi H, Deformation and fragmentation behaviour of exploded metal cylinders and the effects of wall materials, config uration, explosive energy and initiated locations, International Journal of Impact Engineering, 2008, 35(12): 1578-1586.

17 Shapoval A, Mos’pan D, Dragobetskii V, Ensuring high performance characteristics for explosion-welded bimetals, 2016, 60(3-4): 313-317.

18 Choi S J, Lee K H, Gudmestad O T, The effect of dynamic amplification due to a structure׳s vibration on breaking wave impact, Ocean Engineering, 2015, 96: 8-20.

19 Ankang Z, Shihai C, Haixia W, Xiantang Z, Discussion of strain rate of building structure under blasting vibration response, Blasting, 2010, 27(3): 9-12.

20 Chung L, Reinhorn A, Soong T, Experiments on active control of seismic structures, 1988, 114(2): 241-256.

21 Gates W E, Morden M, Professional structural engineering experience related to welded steel moment frames following the Northridge earthquake, The Structural Design of Tall Buildings, 1996, 5(1): 29-44.

22 Gertsch R, Gertsch L, Rostami J, Disc cutting tests in Colorado Red Granite: Implications for TBM performance prediction, International Journal of Rock Mechanics and Mining Sciences, 2007, 44(2): 238-246.

23 Balci C, Correlation of rock cutting tests with field performance of a TBM in a highly fractured rock formation: A case study in Kozyatagi-Kadikoy metro tunnel, Turkey, Tunnelling and Underground Space Technology, 2009, 24(4): 423-435.

24 Gao S, Kang R, Dong Z, Zhang B, Edge chipping of silicon wafers in diamond grinding, International Journal of Machine Tools and Manufacture, 2013, 64: 31-37.

25 Molinari A, Soldani X, Miguélez M, Adiabatic shear banding and scaling laws in chip formation with application to cutting of Ti-6Al-4V, Journal of the Mechanics and Physics of Solids, 2013, 61(11): 2331-2359.

26 Lorentzon J, Järvstråt N, Josefson B, Modelling chip formation of alloy 718, Journal of Materials Processing Technology, 2009, 209(10): 4645-4653.

27 Wang B, Liu Z, Yang Q, Investigations of yield stress, fracture toughness, and energy distribution in high speed orthogonal cutting, International Journal of Machine Tools and Manufacture, 2013, 73: 1-8.

28 Schulz H, Abele E, Sahm, Material aspects of chip formation in HSC machining, CIRP Annals, 2001, 50(1): 45-48.

29 Sutter G, List G, Very high speed cutting of Ti-6Al-4V titanium alloy-change in morphology and mechanism of chip formation, International Journal of Machine Tools and Manufacture, 2013, 66: 37-43.

30 Zhang B, Howes T D, Subsurface evaluation of ground ceramics, CIRP annals, 1995, 44(1): 263-266.

31 Zhou L, Shimizu J, Muroya A, Eda H, Material removal mechanism beyond plastic wave propagation rate, Precision Engineering, 2003, 27(2): 109-116.

32 Masuda K, Mizutani H, Yamada I, Experimental study of strain-rate dependence and pressure dependence of failure properties of granite, Journal of Physics of the Earth, 1987, 35(1): 37-66.

33 Zhang Q B, Zhao J, A review of dynamic experimental techniques and mechanical behaviour of rock materials, Rock mechanics and rock engineering, 2014, 47(4): 1411-1478.

34 Frew D J, Forrestal M J, Chen W, Pulse shaping techniques for testing brittle materials with a split hopkinson pressure bar, Experimental Mechanics, 2002, 42(1): 93-106.

35 Liu W D, Liu K X, Xia X X, The failure stress of bulk metallic glasses under very high strain-rate, Journal of Materials Research, 2010, 25(7): 1230-1234.

36 Liu W D, Liu K X, Mechanical behavior of a Zr-based metallic glass at elevated temperature under high strain-rate, Journal of Applied Physics, 2010, 108(3): 033511.

37 Meyers M, Xu Y, Xue Q, Microstructural evolution in adiabatic shear localization in stainless steel, Acta Materialia, 2003, 51(5): 1307-1325.

38 Wang B, Liu Z, Investigations on deformation and fracture behavior of workpiece material during high speed machining of 7050-T7451 aluminum alloy, CIRP Journal of Manufacturing Science and Technology, 2016, 14: 43-54.

39 Wang B, Liu Z, Investigations on the chip formation mechanism and shear localization sensitivity of high-speed machining Ti-6Al-4V, The International Journal of Advanced Manufacturing Technology, 2014, 75(5-8): 1065-1076.

40 Tian L, Fu Y, Xu J, The influence of speed on material removal mechanism in high speed grinding with single grit, International Journal of Machine Tools and Manufacture, 2015, 89: 192-201.

41 Clifton R J, Klopp R W, Pressure-shear plate impact testing, Metals handbook, 1985, 8(9): 230-239.

42 Nicholas T, Tensile testing of materials at high rates of strain, Experimental mechanics, 1981, 21(5): 177-185.

43 Frew D J, Akers S A, Chen W, Green M L, Development of a dynamic triaxial Kolsky bar, Measurement Science and Technology, 2010, 21(10): 105704.

44 Rome J, Isaacs J, Nemat-Nasser S, Hopkinson techniques for dynamic triaxial compression tests, Recent advances in experimental mechanics, Springer, 2002: 3-12.

45 Xue Q, Meyers M, Nesterenko V, Self-organization of shear bands in titanium and Ti-6Al-4V alloy, Acta Materialia, 2002, 50(3): 575-596.

46 Poulachon G, Moisan A L, Jawahir I, Evaluation of chip morphology in hard turning using constitutive models and material property data, Journal of Manufacturing Science and Engineering, 2007, 129(1): 41-47.

47 Recht R F, Taylor ballistic impact modelling applied to deformation and mass loss determinations, International Journal of Engineering Science, 1978, 16(11): 809-827.

48 Mondal C, Mishra B, Jena P K, Effect of heat treatment on the behavior of an AA7055 aluminum alloy during ballistic impact, International Journal of Impact Engineering, 2011, 38(8-9): 745-754.

49 Johnson G R, A constitutive model and data for materials subjected to large strains, high strain-rates, and high temperatures, Proc 7th Inf Sympo Ballistics, 1983, 541-547.

50 Calamaz M, Coupard D, Girot F, A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti-6Al-4V, International Journal of Machine Tools and Manufacture, 2008, 48(3-4): 275-288.

51 Pan Z, Shih D S, Tabei A, Modeling of Ti-6Al-4V machining force considering material microstructure evolution, The International Journal of Advanced Manufacturing Technology, 2017, 91(5-8): 2673-2680.

52 Rule W K, Jones S, A revised form for the Johnson-Cook strength model, International Journal of Impact Engineering, 1998, 21(8): 609-624.

53 Li G, Prediction of adiabatic shear in high speed machining based on linear perturbation analysis, Dalian University of Technology, 2009.

54 Wang X, Huang C, Zou B, Dynamic behavior and a modified Johnson-Cook constitutive model of Inconel 718 at high strain-rate and elevated temperature, Materials Science and Engineering: A, 2013, 580: 385-390.

55 Lin Y, Chen X M, Liu G, A modified Johnson-Cook model for tensile behaviors of typical high-strength alloy steel, Materials Science and Engineering: A, 2010, 527(26): 6980-6986.

56 Holmquist T J, Johnson G R, A computational constitutive model for glass subjected to large strains, high strain-rates and high pressures, Journal of Applied Mechanics, 2011, 78(5): 051003.

57 Johnson G R, Holmquist T J, An improved computational constitutive model for brittle materials, Proceedings of the AIP Conference Proceedings, AIP, 1994: 981-984.

58 Lv G, Computer simulation of the effect of copper-riched precipitates on hardening and embrittlement in reactor pressure vessel steels, University of science and technology Beijing, 2017.

59 Follansbee P, Kocks U, A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable, Acta Metallurgica, 1988, 36(1): 81-93.

60 Meyers M A, Benson D J, Vöhringer O, Constitutive description of dynamic deformation: physically-based mechanisms, Materials Science and Engineering: A, 2002, 322(1): 194-216.

61 MF A, Thermodynamics and kinetics of slip, Progress in materials science, 1975, 19: 1-281.

62 Clifton R, Analysis of elastic-visco-plastic waves of finite uniaxial strain, 1971.

63 Zerilli F J, Armstrong R W, Dislocation-mechanics-based constitutive relations for material dynamics calculations, Journal of applied physics, 1987, 61(5): 1816-1825.

64 Mecking H, Kocks U, Kinetics of flow and strain-hardening, Acta Metallurgica, 1981, 29(11): 1865-1875.

65 Steinberg D, Lund C, A constitutive model for strain rates from 10^-4 to 10⁶ s^-1, Journal of Applied Physics, 1989, 65(4): 1528-1533.

66 Wedberg D, Lindgren L E, Modelling flow stress of AISI 316L at high strain-rates, Mechanics of Materials, 2015, 91: 194-207.

67 Gao C, Zhang L, Constitutive modelling of plasticity of fcc metals under extremely high strain-rates, International Journal of Plasticity, 2012, 32: 121-133.

68 Galligan J M, McKrell T J, Robson M T, Dislocation drag processes, Materials Science and Engineering: A, 2000, 287(2): 259-264.

69 Tang Y, Uncovering the inertia of dislocation motion and negative mechanical response in crystals, Scientific Reports, 2018, 8(1): 140.

70 Regazzoni G, Kocks U F, Follansbee P S, Dislocation kinetics at high strain-rates, Acta Metallurgica, 1987, 35(12): 2865-2875.

71 Mao Z N, An X H, Liao X Z, Wang J T, Opposite grain size dependence of strain rate sensitivity of copper at low vs high strain-rates, Materials Science and Engineering: A, 2018, 738: 430-438.

72 Wang Q, Liu Z, Microhardness Prediction Based on a Microstructure-Sensitive Flow Stress Model During High Speed Machining Ti-6Al-4V, Journal of Manufacturing Science and Engineering, 2018, 140(9): 091003.

73 Outeiro J, Umbrello D, M’saoubi R, Experimental and numerical modelling of the residual stresses induced in orthogonal cutting of AISI 316L steel, International Journal of Machine Tools and Manufacture, 2006, 46(14): 1786-1794.

74 Johnson G R, Hoegfeldt J, Lindholm U, Nagy A, Response of various metals to large torsional strains over a large range of strain rates-Part 1: Ductile metals, Journal of Engineering Materials and Technology, 1983, 105(1): 42-47.

75 Chiem C, Duffy J, Strain rate history effects and observations of dislocation substructure in aluminum single crystals following dynamic deformation, Materials Science and Engineering, 1983, 57(2): 233-247.

76 Bleck W, Schael I, Determination of crash‐relevant material parameters by dynamic tensile tests, Steel research, 2000, 71(5): 173-178.

77 Grässel O, Krüger L, Frommeyer G, Meyer L, High strength Fe-Mn-(Al, Si) TRIP/TWIP steels development-properties-application, International Journal of plasticity, 2000, 16(10-11): 1391-1409.

78 Boyce B L, Dilmore M F, The dynamic tensile behavior of tough, ultrahigh-strength steels at strain-rates from 0.0002 s^-1 to 200 s^-1, International Journal of Impact Engineering, 2009, 36(2): 263-271.

79 Kim J H, Kim D, Han H N, Barlat F, Strain rate dependent tensile behavior of advanced high strength steels: Experiment and constitutive modeling, Materials Science and Engineering: A, 2013, 559: 222-231.

80 Liu X, Dynamic constitutive relationship of TC4 titanium alloy, Nanjing University of Aeronautics and Astronautics, 2010.

81 Bhat H S, Rosakis A J, Sammis C G, A Micromechanics Based Constitutive Model for Brittle Failure at High strain-rates, Journal of Applied Mechanics, 2012, 79(3): 031016-031012.

82 Rosakis A J, Zehnder A T, On the dynamic fracture of structural metals, International Journal of Fracture, 1985, 27(3): 169-186.

83 Deng X, Rosakis A J, Dynamic crack propagation in elastic-perfectly plastic solids under plane stress conditions, Journal of the Mechanics and Physics of Solids, 1991, 39(5): 683-722.

84 Li X, Li H, Zhang Q, Dynamic fragmentation of rock material: Characteristic size, fragment distribution and pulverization law, Engineering Fracture Mechanics, 2018, 199: 739-759.

85 Zakir S M, Zhen W, Tao S, High Rate Response and Dynamic Failure of Aluminosilicate Glass under Compression Loading, Procedia Structural Integrity, 2018, 13: 1244-1249.

86 Grady D, Kipp M, Mechanisms of dynamic fragmentation: factors governing fragment size, Mechanics of Materials, 1985, 4(3-4): 311-320.

87 Clifton R J, Response of materials under dynamic loading, International Journal of Solids and Structures, 2000, 37(1): 105-113.

88 Nieh T G, Wadsworth J, Homogeneous deformation of bulk metallic glasses, Scripta Materialia, 2006, 54(3): 387-392.

89 Lu J, Ravichandran G, Johnson W L, Deformation behavior of the Zr41.2Ti13.8Cu12.5Ni10Be22.5 bulk metallic glass over a wide range of strain-rates and temperatures, Acta Materialia, 2003, 51(12): 3429-3443.

90 Yu H B, Shen X, Wang Z, Tensile Plasticity in Metallic Glasses with Pronounced β Relaxations, Physical Review Letters, 2012, 108(1): 015504.

91 Turley D M, Doyle E D, Ramalingam S, Calculation of shear strains in chip formation in titanium, Materials Science and Engineering, 1982, 55(1): 45-48.

92 Shaw M C, Cookson J, Metal cutting principles, Oxford university press New York, 2005.

93 Wright T W, Ockendon H, A scaling law for the effect of inertia on the formation of adiabatic shear bands, International Journal of Plasticity, 1996, 12(7): 927-934.

94 Wang B, Liu Z, Song Q, Proper selection of cutting parameters and cutting tool angle to lower the specific cutting energy during high speed machining of 7050-T7451 aluminum alloy, Journal of cleaner production, 2016, 129: 292-304.

95 Ma W, Chen X, Shuang F, The chip-flow behaviors and formation mechanisms in the orthogonal cutting process of Ti-6Al-4V alloy, Journal of the Mechanics and Physics of Solids, 2017, 98: 245-270.

96 Ye G, Xue S, Ma W, Dai L, Onset and evolution of discontinuously segmented chip flow in ultra-high-speed cutting Ti-6Al-4V, The International Journal of Advanced Manufacturing Technology, 2017, 88(1-4): 1161-1174.

97 Zhao D, Sangesland S, Vedvik N, An experimental study of axial vibration assisted drilling, Journal of Natural Gas Science and Engineering, 2016, 35: 1158-1166.

98 Lv D, Huang Y, Wang H, Improvement effects of vibration on cutting force in rotary ultrasonic machining of BK7 glass, Journal of Materials Processing Technology, 2013, 213(9): 1548-1557.

99 Wang J, Zhang C, Feng P, Zhang J, A model for prediction of subsurface damage in rotary ultrasonic face milling of optical K9 glass, The International Journal of Advanced Manufacturing Technology, 2016, 83(1-4): 347-355.

100 Kahraman S, Correlation of TBM and drilling machine performances with rock brittleness, Engineering Geology, 2002, 65(4): 269-283.

101 Gong Q M, Zhao J, Influence of rock brittleness on TBM penetration rate in Singapore granite, Tunnelling and Underground Space Technology, 2007, 22(3): 317-324.

102 Wu W R, Lou L, Liang X J, Cutting features of damage rock by shock disturbance, Journal of Central South University (Science and Technology), 2017, 48: 2709-2714.

103 Zhang Y Q, Lu Y, Hao H, Analysis of fragment size and ejection velocity at high strain-rate, International Journal of Mechanical Sciences, 2004, 46(1): 27-34.

104 Kipp M, Grady D, Dynamic fracture growth and interaction in one dimension, Journal of the Mechanics and Physics of Solids, 1985, 33(4): 399-415.

105 Zhang W, Zhang Y, Zhang G, Single and multiple dynamic impacts behaviour of ultra-high performance cementitious composite, Journal of Wuhan University of Technology-Mater Sci Ed, 2011, 26(6): 1227-1234.

106 Von Karman T, Duwez P, The propagation of plastic deformation in solids, Journal of Applied Physics, 1950, 21(10): 987-994.

107 Wang L, Foundations of stress waves, Elsevier, 2011.

108 Jiang F, Li Z M, Wang N C, Research on dynamic characteristics of Shanxi black granite under high strain-rates, Journal of Vibration and Shock, 2016, 35:177-182.

109 Huang S, Xia K, Zheng H, Observation of microscopic damage accumulation in brittle solids subjected to dynamic compressive loading, Review of Scientific Instruments, 2013, 84(9): 093903.

110 Liu J, Fan Q, Cai H, Wang F, Underlying mechanism of periodical adiabatic shear bands generated in Ti-6Al-4V target by projectile impact, Materials and Design, 2015, 87: 231-237.

111 Zheng C, Wang F, Cheng X, Failure mechanisms in ballistic performance of Ti-6Al-4V targets having equiaxed and lamellar microstructures, International Journal of Impact Engineering, 2015, 85: 161-169.

112 Rice J R, Thomson R, Ductile versus brittle behaviour of crystals, The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics, 1974, 29(1): 73-97.

113 Wang B, Liu Z, Su G, Ai X, Brittle removal mechanism of ductile materials with ultrahigh-speed machining, Journal of Manufacturing Science and Engineering, 2015, 137(6): 061002.

114 Lawn B, Wilshaw T R, Fracture of brittle solids, Cambridge university press, 1993.

115 Armstrong R, Walley S, High strain-rate properties of metals and alloys, International Materials Reviews, 2008, 53(3): 105-128.

116 Mahalingam S, Flewitt P, Knott J, The ductile-brittle transition for nominally pure polycrystalline nickel, Materials Science and Engineering: A, 2013, 564: 342-350.

117 Abushawashi Y, Xiao X, Astakhov V, Modeling of serrated chip formation with a fracture locus approach, Proceedings of the ASME 2011 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, 2011: 373-384.

118 Griffith A A, The phenomena of rupture and flow in solids, Philosophical transactions of the royal society of london Series A, containing papers of a mathematical or physical character, 1921, 221(582-593): 163-198.

119 Orowan E, Fracture and strength of solids, Reports on progress in physics, 1949, 12(1): 185.

120 Stroh A, The formation of cracks as a result of plastic flow, Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1954, 223(1154): 404-414.

121 Cottrell A H, Theory of brittle fracture in steel and similar metals, Trans Met Soc AIME, 1958, 212.

122 Li H, Fan C, Tao K, Compressive Behavior of a Zr-Based Metallic Glass at Cryogenic Temperatures, 2006, 18(6): 752-754.

123 Qiao J C, Wang Q, Pelletier J M, Structural heterogeneities and mechanical behavior of amorphous alloys, Progress in Materials Science, 2019, 104: 250-329.

124 Donovan P E, Stobbs W M, The structure of shear bands in metallic glasses, Acta Metallurgica, 1981, 29(8): 1419-1436.

125 Argon A S, Plastic deformation in metallic glasses, Acta Metallurgica, 1979, 27(1): 47-58.

126 Chen H, He Y, Shiflet G J, Deformation-induced nanocrystal formation in shear bands of amorphous alloys, Nature, 1994, 367(6463): 541-543.

127 Zhang B, Yin J, The ‘skin effect’ of subsurface damage distribution in materials subjected to high-speed machining, International Journal of Extreme Manufacturing, 2019, 1(1): 012007.

128 Jones R E, Fatigue crack growth retardation after single-cycle peak overload in Ti-6Al-4V titanium alloy, Engineering Fracture Mechanics, 1973, 5(3): 585-604.

129 Krishnan K, Sockalingam S, Bansal S, Numerical simulation of ceramic composite armor subjected to ballistic impact, Composites Part B: Engineering, 2010, 41(8): 583-593.

130 Crouch I G, Kesharaju M, Nagarajah R, Characterisation, significance and detection of manufacturing defects in Reaction Sintered Silicon Carbide armour materials, Ceramics International, 2015, 41(9, Part B): 11581-11591.

131 Lundberg P, Interface defeat and penetration: two modes of interaction between metallic projectiles and ceramic targets, Acta Universitatis Upsaliensis, 2004.

132 Salomon C, Process for the machining of metals of similarly acting materials when being worked by cutting tools: German, 523594.